3D Artworks with Rhino, Grasshopper, and Photoshop
with links to academic papers
A Virtual Chain Mail Pseudosphere

During the Illustrating Mathematics semester at ICERM in Fall 2019, I learned to use the architectural design program Rhino with a very mathematical plug-in called Grasshopper to make virtual objects based on mathematical formulas.
I had nearly finished a project with SCU student Wilder Boyden to weave bands (virtually) into shapes with any given polyhedral symmetry. The new technique provided satisfying new images to illustrate that article. I continued with virtual chain mail, knitting, weaving, and the list goes on.
During the pandemic, our community of researchers reminded one another how lucky we had been to be together in person that autumn in Rhode Island!
Although I have indeed printed some of these objects, my enjoyment of the shapes derives from placing them in virtual environments.
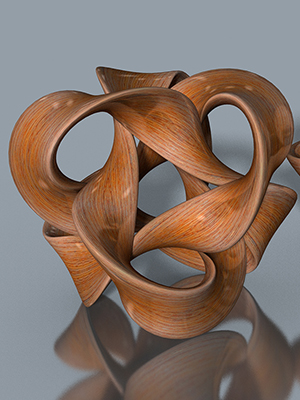
"Woven" Polyhedra
Doesn't it look real? This image shows an object made from three bands (each with D2 symmetry), mathematically arranged to produce tetrahedral symmetry. Read more in "Polyhedral Symmetry from Tubes and Ribbons" in the Journal of Mathematics and the Arts. (This appears to be behind a paywall, but you can access the JMA with your MAA membership!

Chain mail referencing wallpaper pattern type cmm
The techniques of Fourier series that I developed in my very first symmetry-related article, "Surprising Symmetry: Wheels on Wheels on Wheels" in Mathematics Magazine, turn out to be just right for designing chain mail patterns. Although Bridges was moved online in 2020, I still presented a paper, "Wallpaper patterns from non-planar chain mail links." It's one of my favorites.
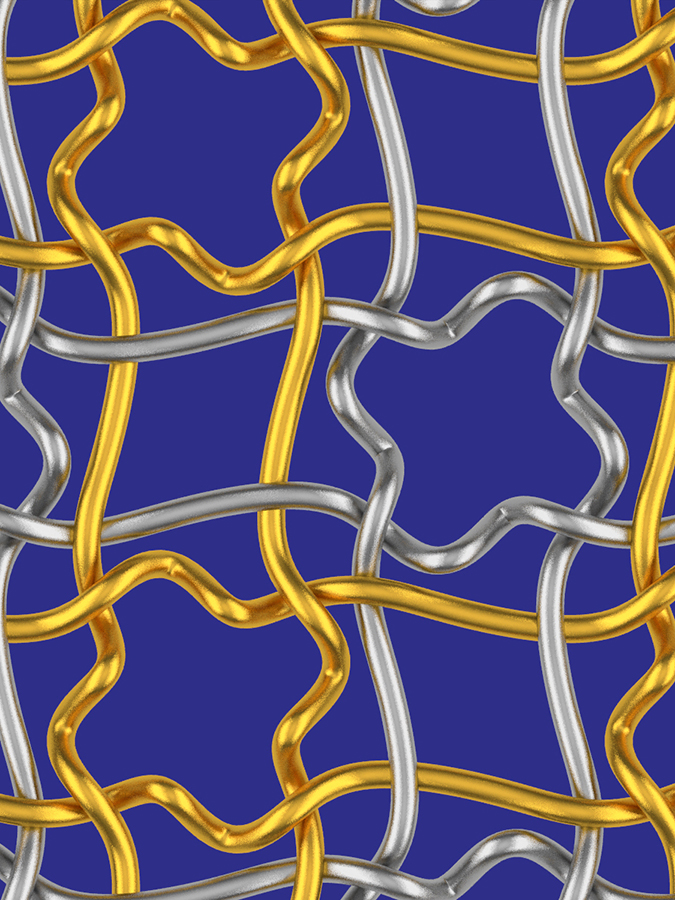
A woven pattern symmetric under the layer group p4g/p4
For Bridges 2021, again held online, I nailed down some details I had referred to in the chain mail paper: Rather than talking about wallpaper symmetry for these patterns, we should say that they are invariant under the layer groups, which are groups of isometries of space that fix a plane, in this case the plane of the pattern. This increases the 17 possibilities for mere wallpaper to 80 pattern types for woven patterns. The paper is called "Wallpaper Patterns from Looping Strands: The Layer Groups."

A 7-color torus
This pattern illustrates the famous theorem that a map on the torus may require 7 colors. The knots might represent countries and you can see that each knot is surrounded by six others of different colors. Click on the image and you may see why this represents a torus: If we identify shapes of the same color, the resulting space folds into a torus. Read about this in Math Horizons: "It Takes Seven Colors to Color a Torus."